[통계] R과 Excel을 이용하여 평균(mean), 분산(variance), 표준편차(Standard deviation) 구하는 방법

평균, 분산, 표준편차 개념 및 계산 방법

 
빅데이터에서 통계학은 필수가 아닐 수 없습니다.
통계에서 자주 쓰이는 평균, 분산 그리고 표준편차 구하는 방법에 대해 알려드리겠습니다.

우선적으로 빅데이터 연구에서 많이 사용하는 R과 Excel에서 평균, 분산 그리고 표준편차를 계산하는 방법에 대해 알아보겠습니다.

# 평균 계산

R을 이용해 평균을 계산해 보겠습니다.
Rstudio에 다음을 입력합니다.

x <- c(1,2,4)
mean(x) # 평균

R을 이용한 평균

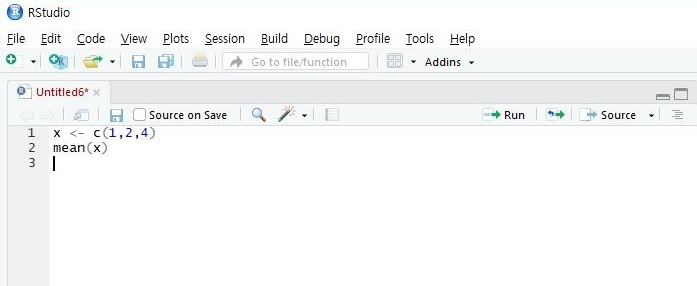
전체 영역을 선택한 후 오른쪽에 Run (Ctrl + Enter)을 누릅니다.

R mean

다음과 같이 평균 결괏값이 2.333333 이 출력되었습니다.

학창 시절 배운 평균을 계산해 보면
1+2+4 = 7입니다.
7을 3으로 나눈 값은 2.3333333333333 이 됨을 알 수 있으실 겁니다.

계산기를 통한 평균

위 값은 암산이 가능하겠지만 여러 인자의 평균을 구할 경우에는 프로그램의 사용이 훨씬 효율적일 겁니다.

이번에는 엑셀(Excel)을 사용해 보겠습니다.
엑셀은 AVERAGE 함수를 사용하여 평균을 구합니다.

1, 2, 3의 평균으로 2.33333 결괏값으로 나왔습니다.

Excel을 통한 평균

 

# 분산 계산

분산을 왜 계산하는 걸까요?
분산의 사전적 의미를 먼저 확인해 보겠습니다.
분산: 갈라져 흩어짐. 즉 흩어져 있는 것을 분산이라고 합니다.

분산은 얼마나 흩어져 있는지, 불규칙하게 분포되어 있는지를 나타냅니다.
분산 값이 클수록 집단의 변화가 크고 그만큼 평균으로부터 퍼져있다고 할 수 있습니다.
분산이 줄어들수록 정밀도가 증가합니다.

위 설명처럼 분산이란 인자와 평균값이 얼마나 차이가 나는지를 계산하는 방법입니다.

앞서 했던 평균 계산을 예를 들어보겠습니다.

x의 인자는 1, 2, 4 가 있습니다.
x의 평균은 2.3333입니다.
각각의 인자와 평균의 차이는 다음과 같습니다.

1 - 2.3333 = -1.3333
2 - 2.3333 = -0.3333
4 - 2.3333 = 1.6667

먼저 위 값들을 제곱을 구합니다.

-1.33332 = 1.77768889
-0.33332 = 0.11108889
1.66672 = 2.77788889

이후 결과를 더합니다.

1.77768889 + 0.11108889 + 2.77788889 = 4.66666667

위 값을 (n-1)로 나눈 값이 분산이 됩니다.
4.66666667 / (3 -1) = 2.333333335 <== 분산(variance)

R을 이용하여 분산을 구해보겠습니다.

R을 이용한 분산

Excel을 이용하여 분산을 계산해보겠습니다.

Excel을 이용한 분산

R과 Excel 둘 다 VAR 함수를 이용하여 분산을 구하는 것을 알 수 있습니다.

# 표준편차

이번에는 표준편차에 대해 알아보겠습니다. 실제 통계에서는 분산보다는 표준편차를 사용합니다.
표준편차는 분산을 제곱근 합니다.
분산은 제곱을 하기 때문에 값이 부풀려집니다.
표준편차는 부풀려진 분산을 원래 크기로 만들어 줍니다.

R로 표준편차를 구해보겠습니다.

R을 이용한 표준편차

sd 함수를 사용하여 표준편차를 구할 수 있습니다.

다음은 엑셀을 이용하여 표준편차를 구해보겠습니다.

Excel을 이용한 표준편차

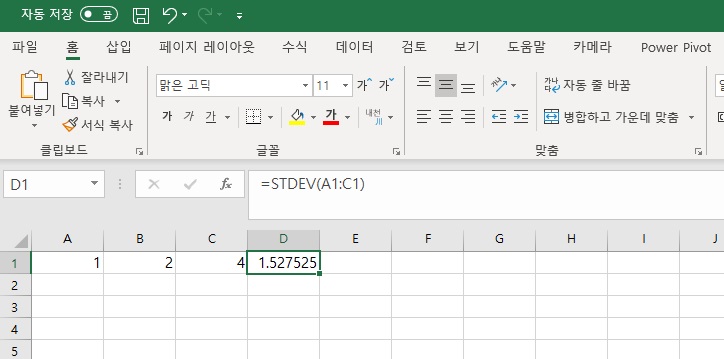
Excel은 STDEV 수식을 이용하여 표준편차를 계산합니다.


이상 통계에서 가장 자주 사용하는 평균, 분산, 표준편차에 대해 알아보았습니다.